Bài trước những em vẫn biết lúc nào hàm số đồng trở nên và lúc nào hàm số nghịch tặc trở nên. thạo được quy tác xét tính đơn điệu (đồng trở nên, nghịch tặc trở nên của hàm số.
Bài này những em tiếp tục biết rất rất trị của hàm số là gì? nhị cơ hội (quy tắc) dò la rất rất trị của hàm số được tiến hành như vậy nào?
Bạn đang xem: giá trị cực đại là y hay x
• Bài tập luyện áp dụng quy tắc dò la rất rất trị của hàm số
I. Khái niệm cực lớn rất rất tè của hàm số
* Định nghĩa cực lớn, rất rất tiểu
• Cho hàm số nó = f(x) xác lập và liên tiếp bên trên khoảng chừng (a ; b) và điểm x0 ∈ (a ; b).
- Nếu tồn bên trên số h > 0 sao cho f(x) < f(x0), ∀x ∈ (x0 - h ; x0 + h), x ≠ x0 thì tớ trình bày hàm số f đạt cực đại tại x0 .
- Nếu tồn bên trên số h > 0 sao cho f(x) > f(x0), ∀x ∈ (x0 - h ; x0 + h), x ≠ x0 thì tớ trình bày hàm số f đạt cực tiểu tại x0.
> Chú ý:
- Nếu hàm số f(x) đạt cực lớn (cực tiểu) bên trên x0 thì x0 được gọi là vấn đề cực lớn (điểm rất rất tiểu) của hàm số; f(x0) được gọi là độ quý hiếm cực lớn (giá trị rất rất tiểu) của hàm số, ký hiệu fCĐ (fCT), còn điểm M(x0; f(x0)) được gọi là vấn đề cực lớn (điểm rất rất tiểu) của thiết bị thị.
- Các điểm cực lớn và rất rất tè được gọi công cộng là vấn đề rất rất trị. Giá trị cực lớn (giá trị rất rất tiểu) thường hay gọi là cực lớn (cực tiểu) và được gọi công cộng là rất rất trị của hàm số.
- Nếu hàm số nó = f(x) với đạo hàm bên trên khoảng chừng (a;b) và đạt cực lớn hoặc rất rất tè bên trên x0 thì f'(x0) = 0.
II. Điều khiếu nại đầy đủ nhằm hàm số với rất rất trị (cực đại, rất rất tiểu)
• Định lý 1: Cho hàm Cho hàm số nó = f(x) liên tiếp bên trên khoảng chừng K = (x0 - h ; x0 + h) (h > 0) và với đạo hàm bên trên K hoặc bên trên K\{x0}.
- Nếu thì x0 là vấn đề cực lớn của hàm số.
- Nếu thì x0 là điểm rất rất tè của hàm số.
Có thể hiểu giản dị, lên đường kể từ trái ngược qua chuyện phải:
- Nếu f'(x) thay đổi vệt kể từ - quý phái + khi trải qua x0 thì x0 là vấn đề rất rất tè.
- Nếu f'(x) thay đổi vệt kể từ + quý phái - khi trải qua x0 thì x0 là điểm rất rất tè.
• Định lý 2: Cho hàm số y = f(x) với đạo hàm cấp cho nhị bên trên khoảng K = (x0 - h ; x0 + h) (h > 0).
- Nếu f'(x0) = 0, f''(x0) > 0 thì x0 là điểm rất rất tè của hàm số f.
- Nếu f'(x0) = 0, f''(x0) < 0 thì x0 là điểm cực lớn của hàm số f.
III. Cách dò la rất rất trị của hàm số, quy tắc dò la rất rất trị của hàm số
• Quy tắc 1 (cách 1) nhằm dò la rất rất trị của hàm số
- Tìm tập luyện xác lập.
- Tính f'(x). Tìm những điểm bên trên ê f'(x) vày 0 hoặc f'(x) ko xác lập.
- Lập bảng trở nên thiên.
- Từ bảng trở nên thiên suy rời khỏi những điểm rất rất trị.
• Quy tắc 2 (cách 2) nhằm dò la rất rất trị của hàm số
- Tìm tập luyện xác lập.
- Tính f'(x). Tìm những nghiệm xi của phương trình f'(x)=0.
Xem thêm: CaKhia TV - Địa chỉ trực tiếp bóng đá uy tín nhất hiện nay
- Tính f''(x) và f''(xi) suy rời khỏi đặc điểm rất rất trị của những điểm xi.
> Chú ý: Nếu f''(xi)=0 thì tớ nên sử dụng quy tắc 1 nhằm xét rất rất trị bên trên xi.
* Ví dụ 1: sít dụng quy tắc 1 (cách 1) dò la rất rất trị của hàm số f(x) = x(x2 - 3).
> Lời giải:
1. TXĐ: D = R
2. f’(x) = 3x^2 – 3. Cho f’(x) = 0 ⇔ x = 1 hoặc x = -1.
3. Ta với bảng trở nên thiên: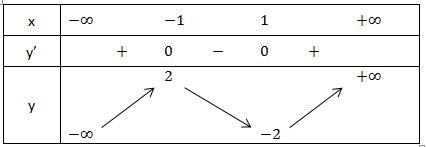
Hàm số đạt cực lớn bên trên x = -1 và độ quý hiếm cực lớn là 2
Hàm số đạt rất rất tè bên trên x = 1 và độ quý hiếm rất rất tè là -2.
* Ví dụ 2: sít dụng quy tắc 2 (cách 2) dò la rất rất trị của hàm số:
> Lời giải:
1. TXĐ:D = R
2. Ta tính f'(x) = x3 - 4x = x(x2 - 4);
Cho f'(x) = 0 ⇔ x1 = 0; x2 = -2; x3 = 2.
- Tính f''(x) = 3x2 - 4. tớ có:
f''(x1) = f''(0) = 2.02 - 4 = -4<0 ⇒ x1 = 0 là vấn đề rất rất đại
f''(x2) = f''(-2) = 3.(-2)2 - 4 =8 ⇒ x2 = -2 là vấn đề cực tiểu
f''(x3) = f''(2) = 3.(2)2 - 4 =8 ⇒ x3 = 2 là vấn đề cực tiểu
- Kết luận: f(x) đạt cực lớn bên trên x1 = 0 và fCĐ = f(0) = 6;
f(x) đạt rất rất tè bên trên x2 = -2, x3 = 2 và fCT = f(±2) = 2.
* Ví dụ 3: Tìm những điểm rất rất trị của hàm số nó = sin2x.
> Lời giải:
- TXĐ: D = R
- Ta có: f'(x) = 2cos2x; mang đến f'(x) = 0 ⇔ cos2x = 0
- Lại có: f''(x) = -4sin2x
- Kết luận:
Xem thêm: rút ra một lá bài từ bộ bài 52 lá xác suất để được lá bích là
là những điểm cực lớn của hàm số
là những điểm rất rất tè của hàm số.
Trên đó là nội dung bài viết Cực trị của hàm số là gì? Cách dò la cực lớn, rất rất tè của hàm số. KhoiA kỳ vọng qua chuyện nội dung bài viết này những em đã hiểu rõ được kỹ năng lý thuyết nhằm vận dụng thực hiện những bài bác tập luyện áp dụng. Mọi hùn ý nhằm nội dung bài viết chất lượng tốt rộng lớn những em hãy nhằm lại bên dưới phần phản hồi, KhoiA xin xỏ cảm ơn.











Bình luận