đường cao tam giác vuông

Tam giác vuông là 1 trong những trong mỗi hình học tập cơ phiên bản nhập toán học tập, và lối cao là 1 trong những định nghĩa cần thiết trong các công việc đo lường diện tích S của tam giác. Tuy nhiên, nhằm tính được lối cao của một tam giác vuông ko cần là vấn đề giản dị. Trong nội dung bài viết này, tất cả chúng ta tiếp tục nằm trong Dapanchuan.com lần hiểu về toan lý, đặc thù rưa rứa phương pháp tính lối cao nhập tam giác vuông, giúp cho bạn nắm rõ rộng lớn về định nghĩa này và phần mềm trong số việc hình học tập và toán học tập phần mềm.

Đường cao nhập tam giác vuông là gì?

Đường cao nhập một tam giác vuông là đoạn trực tiếp nối đỉnh của góc vuông với đối lập của chính nó bên trên cạnh huyền. Nó được gọi là lối cao vì thế này là lối đi kể từ đỉnh của góc vuông xuống đối lập của chính nó, và bên cạnh đó cũng chính là lối cao của hình chiếu vuông góc của đỉnh cơ lên cạnh đối lập. Đường cao nhập một tam giác vuông cũng chính là nửa đường kính của lối tròn trĩnh nội tiếp của tam giác.

Bạn đang xem: đường cao tam giác vuông

Định lý về lối cao nhập tam giác vuông

Định lý lối cao nhập tam giác vuông là 1 trong những trong mỗi toan lý cần thiết nhập hình học tập tam giác và được dùng thoáng rộng trong số việc tương quan cho tới tam giác vuông.

Định lý lối cao nhập tam giác vuông thưa rằng: “Trong một tam giác vuông, lối cao còn là một tầm hình học tập và trung vị của cạnh huyền.”

Cụ thể rộng lớn, fake sử nhập tam giác vuông ABC đem cạnh huyền BC, lối cao AH hạ xuống cạnh AB, và gọi M là trung điểm của cạnh BC. Khi cơ, tớ có:

• Độ lâu năm lối cao AH vì chưng tích của chừng lâu năm cạnh huyền BC và chừng lâu năm cạnh góc vuông AB, phân tách mang lại chừng lâu năm đoạn trực tiếp AC: AH = (BC x AB) / AC
• Độ lâu năm lối cao AH vì chưng chừng lâu năm đoạn trực tiếp BM: AH = BM = MC
• Độ lâu năm lối cao AH cũng chính là tầm nằm trong của nhị cạnh góc vuông AB và BC: AH = (AB + BC) / 2

Định lý lối cao nhập tam giác vuông là 1 trong những khí cụ cần thiết trong các công việc đo lường những thông số kỹ thuật của tam giác vuông, rưa rứa trong các công việc xử lý những việc hình học tập tương quan cho tới tam giác vuông.

Tính hóa học của lối cao nhập tam giác vuông

Tam giác vuông là 1 trong những loại tam giác quan trọng mang trong mình một góc vuông. Vấn đề này kéo đến những đặc thù quan trọng của lối cao nhập tam giác vuông. Những đặc thù này vô cùng hữu ích nhập quy trình giải những bài xích tập luyện và cũng đều có phần mềm nhập cuộc sống đời thường. Sau đấy là những đặc thù cần thiết ghi lưu giữ về lối cao nhập tam giác vuông:

• Tính hóa học loại nhất: Trong tam giác vuông, tích của chừng lâu năm lối cao với chừng lâu năm cạnh huyền ứng vì chưng tích của nhị chừng lâu năm cạnh góc vuông nhập tam giác.
• Tính hóa học loại hai: Trong tam giác vuông, bình phương của chừng lâu năm cạnh góc vuông vì chưng tích của chừng lâu năm cạnh huyền và chừng lâu năm lối cao ứng chiếu lên cạnh huyền.
• Tính hóa học loại ba: Trong tam giác vuông, bình phương của chừng lâu năm lối cao bên trên cạnh huyền vì chưng tích của chừng lâu năm nhị hình chiếu của nhị cạnh góc vuông lên cạnh huyền.
• Tính hóa học loại tư: Trong tam giác vuông, nghịch ngợm hòn đảo của bình phương từng cạnh góc vuông vì chưng nghịch ngợm hòn đảo của bình phương chừng lâu năm lối cao.

Cách tính lối cao nhập tam giác vuông

Dựa nhập công thức tính cạnh nằm trong lối cao nhập tam giác vuông, tớ đem công thức tính lối cao nhập dạng tam giác vuông như sau:

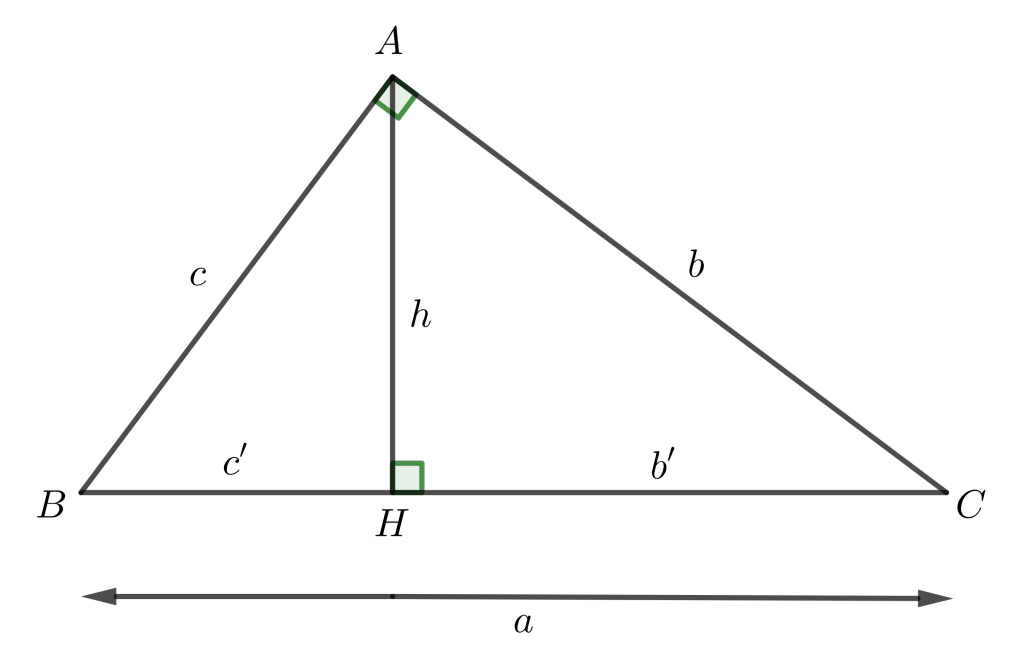
• a² = b² – c²
• b² = a.b′ và c²= a.c′
• a.h= b.c
• h²= b′.c′
• 1/b²=1/b²+1/c²

Trong đó:

• a, b, c: chừng lâu năm những cạnh nằm trong tam giác vuông.
• b’: lối chiếu của cạnh b ứng bên trên cạnh huyền.
• c’: lối chiếu của cạnh c ứng bên trên cạnh huyền.
• h: lối cao hạ xuống kể từ đỉnh góc vuông.

Bài tập luyện tương quan cho tới lối cao nhập tam giác vuông

1. Cho hình △ABC vuông bên trên A đem lối cao AH (H ∊ BC), biết BH= 9m, BC= 25m. Tính chừng lâu năm những lối cao nhập △ABC?
Lời giải tham ô khảo:

H ∊ BC tuy nhiên BH= 9m, BC= 25m

⇒ CH= 25 – 9 = 16 (m)

Áp dụng công thức tính cạnh và lối cao nhập tam giác vuông tớ có:

*) AH² = BH x CH = 9 x 16 = 144

⇒ AH = 12 (m)

*) AB² = BC x BH = 25 x 9 = 225

⇒ AB = 15 (m)

*) AC² = BC x CH = 25 x 16 = 400

Xem thêm: XoilacTV: Nền tảng cập nhật kết quả bóng đá trực tuyến chính xác và mới nhất

⇒ AC = đôi mươi (m)

Vậy chừng lâu năm 3 lối cao nhập △ABC vuông bên trên A: AB, AC, AH thứu tự là 15m, 20m, 12m.

2. Cho tam giác ABC đem góc vuông bên trên A, AB=24cm và AC=32cm. Đường trung trực của BC tiếp tục tách AC, BC theo đòi trật tự là D và E. Tính DE.

Giải:

Xét nhập tam giác vuông ABC, tớ có:

BC2 = AB2+ AC2 ( theo đòi toan lý py-ta-go)

BC2 = 242+ 322

BC2 = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20(cm)

Xét theo đòi tam giác vuông Ngân Hàng Á Châu và tam giác vuông ECD có:

Có góc A = góc E = 90o và góc C công cộng.

=> Tam giác Ngân Hàng Á Châu ∾ tam giác ECD

=> AC/EC = AB/ED

Xem thêm: CaKhia TV - Địa chỉ trực tiếp bóng đá uy tín nhất hiện nay

=> ED = AB.EC/AC = 15cm

Vậy ED = 15cm.

Như vậy, qua chuyện nội dung bài viết này tất cả chúng ta và đã được lần hiểu về những toan lý, đặc thù và phương pháp tính lối cao nhập tam giác vuông. Đường cao không những là 1 trong những định nghĩa cần thiết nhập hình học tập mà còn phải được phần mềm thật nhiều trong số việc thực tiễn. Chắc chắn rằng, Lúc nắm rõ kỹ năng và kiến thức này, các bạn sẽ rất có thể xử lý được rất nhiều việc tương quan cho tới tam giác vuông một cơ hội dễ dàng và đơn giản và hiệu suất cao rộng lớn.