z là tập hợp gì

Tập thích hợp Z hoặc thường hay gọi là hội tụ số vẹn toàn là một trong những hội tụ số đương nhiên phổ cập vô toán học tập. Bài viết lách sau đây IMO2007 tiếp tục trình diễn cho tới chúng ta học viên cụ thể về khái niệm, những hội tụ con cái của Z và một trong những vấn đề áp dụng.

Tập thích hợp Z được khái niệm một cơ hội đơn giản và giản dị là hoàn toàn có thể viết lách được nhưng mà không tồn tại bộ phận phân số. Tập thích hợp Z là hội tụ số vẹn toàn đã cho thấy số vẹn toàn là miền xác lập độc nhất nhưng mà những thành phần dương vô này được bố trí trật tự chất lượng và được bảo toàn bên dưới luật lệ nằm trong.

Bạn đang xem: z là tập hợp gì

Tập thích hợp những số vẹn toàn Z bao hàm số 0, những số đương nhiên dương (1,2,3,…) và những nghịch ngợm hòn đảo luật lệ nằm trong của bọn chúng (các số vẹn toàn âm -1;-2;-3,…).

Tập thích hợp số vẹn toàn Z thông thường được biểu thị bằng văn bản in đậm (Z) hoặc chữ rộng lớn đem viền (). Kí tự động này được bắt mối cung cấp kể từ giờ Đức Zahlen (Có tức là “số”)

là một trong những hội tụ con cái của hội tụ số hữu tỷ và cũng chính là hội tụ con cái của tập luyện số thực .

Tương tự động như các hội tụ số đương nhiên không giống thì hội tụ là hội tụ vô hạn kiểm đếm được.

Kí hiệu hội tụ Z

Biểu tượng còn được dùng để làm biểu thị một trong những hội tụ không giống nhau với cơ hội dùng không giống nhau. Chẳng hạn tất cả chúng ta đem một trong những tình huống sau đây:

Các kí hiệu hội tụ này hoàn toàn có thể không giống nhau bám theo từng đối tượng người dùng dùng. Một số người tiêu dùng kí hiệu mang đến số vẹn toàn không giống 0 tuy nhiên một trong những lại sử dụng nhằm biểu thị cho những số vẹn toàn ko âm.

Tính hóa học của số nguyên

Tương tự động như các hội tụ số không giống thì là hội tụ đóng góp với những luật lệ toán nằm trong trừ nhân phân chia. Vấn đề này Có nghĩa là tổng và tích của nhị số vẹn toàn bất kì là một trong những vẹn toàn. Tuy nhiên, việc bao hàm cả những số vẹn toàn âm, số 0 tiếp tục khiến cho không như những số đương nhiên và cũng chính là hội tụ đóng góp với những luật lệ toán trừ.

Các số vẹn toàn tạo nên trở thành một đai đơn vị chức năng và là đai cơ phiên bản nhất. Vành đơn vị chức năng này nếu như mang 1 luật lệ đồng cấu độc nhất kể từ những số vẹn toàn.

Tập thích hợp ko đóng góp với luật lệ phân chia vì như thế thương của bọn chúng ko hẳn là một trong những vẹn toàn. Ví dụ một là số vẹn toàn, 2 là số vẹn toàn tuy nhiên 1 phân chia 2 ko nên là số vẹn toàn.

Mối quan tiền thông số vẹn toàn và số hữu tỉ

Trong toán học tập, những số vẹn toàn tạo nên trở thành một group nhỏ nhất và đai nhỏ nhất này sẽ tạo nên trở thành những số đương nhiên. Theo lý thuyết đại số thì những số vẹn toàn cơ nhiều lúc được xem như là số hữu tỉ nhằm các bạn dễ dàng và đơn giản phân biệt được với những số vẹn toàn đại số tổng quát lác rộng lớn. Trong thực tiễn, số vẹn toàn (hữu tỉ) là số vẹn toàn đại số và cũng mặt khác là số hữu tỉ. Chúng tớ hoàn toàn có thể bám theo dõi đặc thù cơ phiên bản của số vẹn toàn bám theo bảng sau:

	Phép cộng	Phép nhân
Tính đóng
Tính kết hợp
Tính kí thác hoán
Phần tử đơn vị
Phần tử nghịch ngợm đảo		Số vẹn toàn độc nhất đem thành phần nghịch ngợm hòn đảo là -1 và 1
Thuộc tính phân phối	và
Không đem ước của số 0		Nếu , thì hoặc hoặc cả nhị.

Thuộc tính về lý thuyết loại tự

Tập thích hợp Z là một trong những hội tụ số không tồn tại bất kì số lượng giới hạn bên trên hoặc bên dưới. Ví dụ về trật tự của hội tụ Z được hiểu như sau: .

Một số vẹn toàn dương Khi nó to hơn 0 và vẹn toàn âm Khi nó nhỏ rộng lớn 0.

Số 0 là số trung gian ngoan và nó ko âm cũng ko dương.

Từ trật tự của những số vẹn toàn tớ đem đặc thù sau:

thì tất cả chúng ta đem nhị tính chất:

Do những đặc thù cơ, người tớ tóm lại rằng Z cùng theo với trật tự bên trên là một trong những đai đem trật tự.

Câu căn vặn ôn tập luyện lại lý thuyết

Câu 1: Lấy VD thực tiễn vô cơ đem số vẹn toàn âm, lý giải chân thành và ý nghĩa của số vẹn toàn âm cơ.

Câu 2: Tập thích hợp Z những số vẹn toàn bao hàm những số nào?

Câu 3: Cho biết bên trên trục số nhị số đối nhau đem Điểm sáng gì?

Câu 4: Nói hội tụ Z bao hàm nhị phần tử là số đương nhiên và số vẹn toàn âm đích thị không?

Câu 5: Nhắc lại cơ hội đối chiếu nhị số vẹn toàn a và b bên trên trục số?

Bài tập luyện về hội tụ số nguyên

Để kết đốc lại đề chính này, tất cả chúng ta nằm trong mò mẫm hiểu một số

Bài 1: Cho hội tụ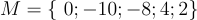

Đề bài

a/ Viết hội tụ N bao gồm những thành phần là số đối của những thành phần nằm trong tập luyện M.

b/ Viết hội tụ P.. bao gồm những thành phần của M và N

Đáp án

a)

b)

Bài 2: Trong những câu sau câu này đúng? Câu này sai?

Đề bài

a/ Mọi số đương nhiên đều là số vẹn toàn.

b/ Mọi số vẹn toàn đều là số đương nhiên.

c/ Có những số vẹn toàn mặt khác là số đương nhiên.

d/ Có những số vẹn toàn ko là số đương nhiên.

e/ Số đối của 0 là 0, số đối của a là (–a).

g/ Khi trình diễn những số (-5) và (-3) bên trên trục số thì điểm (-3) ở phía trái điểm (-5).

h/ Có những số ko là số đương nhiên cũng ko là số vẹn toàn.

Đáp án

ĐS: Các câu sai: b/ g/

Bài 3: Trong những câu sau câu này đúng? Câu này sai?

Đề bài

a/ Bất kỳ số vẹn toàn dương này xũng to hơn số vẹn toàn ân.

b/ Bất kỳ số đương nhiên nào thì cũng to hơn số vẹn toàn âm.

c/ Bất kỳ số vẹn toàn dương nào thì cũng to hơn số đương nhiên.

Xem thêm: CaKhia TV - Địa chỉ trực tiếp bóng đá uy tín nhất hiện nay

d/ Bất kỳ số đương nhiên nào thì cũng to hơn số vẹn toàn dương.

e/ Bất kỳ số vẹn toàn âm nào thì cũng nhỏ rộng lớn 0.

Đáp án

ĐS: Các câu sai: d/

Bài 4: Sắp xếp số nguyên

Đề bài

a/ Sắp xếp những số vẹn toàn sau bám theo trật tự tăng dần: 2, 0, -1, -5, -17, 8

b/ Sắp xếp những số vẹn toàn sau bám theo trật tự hạn chế dần: -103, -2004, 15, 9, -5, 2004

Đáp án

a/ -17. -5, -1, 0, 2, 8

b/ 2004, 15, 9, -5, -103, -2004

Bài 5: Trong những cơ hội viết lách sau, cơ hội viết lách này đúng?

Đề bài

a/ -3 < 0

b/ 5 > -5

c/ -12 > -11

d/ |9| = 9

e/ |-2004| < 2004

f/ |-16| < |-15|

Đáp số

Các câu sai: c/ e/ f/

Bài 6: Tìm x

Đề bài

a/ |x – 5| = 3

b/ |1 – x| = 7

c/ |2x + 5| = 1

Hướng dẫn

a/ |x – 5| = 3 nên x – 5 = ± 3

• x – 5 = 3   ➡ x = 8
• x – 5 = -3  ➡ x = 2

b/ |1 – x| = 7 nên 1 – x = ± 7

• 1 – x = 7   ➡ x = -6
• 1 – x = -7  ➡ x = 8

c/ x = -2, x = 3

Bài 7: So sánh những số sau

Đề bài

a) So sánh và

b) So sánh và

Đáp án

a)

Ta đem

Ta đem

Do cơ

b)

Ta đem

Ta đem

Vì nên

Do cơ

Tài liệu về hội tụ Z

Dưới đó là tổ hợp phần lý thuyết và một trong những dạng toán hoặc về hội tụ số vẹn toàn. Quý Khách hoàn toàn có thể bám theo dõi thẳng bên trên trang web nhé:

Xem thêm: dạng địa hình nào sau đây của nước ta thuận lợi nhất để nuôi trồng thủy sản nước lợ

Trên đó là toàn cỗ kỹ năng về tập thích hợp Z. Mong rằng nội dung bài viết bên trên tăng thêm ý nghĩa với chúng ta fan hâm mộ và gom fan hâm mộ lý giải được số vẹn toàn là gì, cơ hội áp dụng số vẹn toàn vô những vấn đề ra làm sao.